筒仓是散装物料的贮存设施,具有结构简单、占地面积小、空间利用率高、使用方便等特点,广泛应用于粮食、化工等行业。筒仓动态侧压力是指筒仓在卸料过程中由于颗粒之间的相互摩擦和挤压对仓壁产生的侧压力 [1],为筒仓设计中需要考虑的重要参数,其计算结果直接关系到筒仓结构的安全、经济、合理。
近年来,相关学者对立筒仓卸料时的动态侧压力分布规律进行了一系列研究。Gallego 等 [2] 通过离散元软件模拟筒仓中心卸料过程对动态侧压力分布规律及物料流动状态进行研究,与试验结果较为一致。Li 等 [3] 研究得出不同摩擦系数对贮料流态存在很大影响。钟佳等 [4-8] 选用不同结构形式筒仓探究颗粒的流动特性及结构强度,减小了颗粒对筒壁的作用力。Sun 等 [9] 对带地上输送通道的深蹲筒仓充填与排料多尺度试验研究,发现通道顶壁和侧壁均存在超压现象。Gandia 等 [10,11] 采用中试筒仓,研究了玉米在筒仓内填充、静态和放电阶段的最大值和动态侧压力,评估了法向压力和摩擦压力,其结果与欧洲规范对比验证了中试筒仓校准的准确性。郭建玮等 [12-15] 通过对比不同形状、不同性质颗粒的卸料特性,客观反应了卸粮过程的侧压力、颗粒结构、细观力学参数动态变化。综上可知,粮食贮料对仓体的作用是筒仓结构进行受力分析和设计的关键问题,不同种类贮料具有不同的材料属性、内摩擦角和摩擦系数等,都会对仓壁侧压力产生不同的影响,并且现有研究中,这些因素对筒仓动态侧压力与超压系数的影响规律尚不完善。
本文采用EDEM 仿真模拟,选取玉米、小麦和稻谷三种粮食进行数值模拟,研究不同种类贮料物理特性和接触属性下的静态侧压力分布,并与规范计算值进行对比;分析动态侧压力分布规律和相应超压系数、流动状态与速度分布关系;基于灰色关联度分析法进行卸料时动态侧压力影响因素分析,旨在优化筒仓设计并为其实际工程应用提供理论参考。
1 离散元模型建立
1.1 立筒仓模型
EDEM 是基于离散元对煤、矿砂、纤维、谷粒等颗粒物的行为进行仿真分析的软件,通过模拟散装颗粒物料在运输和加工处理等过程中颗粒体系的受力、运动轨迹等其他行为特征,从而更好的分析颗粒与结构和设备之间的相互作用,进而为结构和设备进行设计、测试和优化。因此采用EDEM 离散元软件,以某粮库柱承式立筒仓为研究对象,在本课题组已开展的试验研究 [16] 基础上建立模型。立筒仓采用有机玻璃材料属性,其泊松比为0.33,密度为1 180 kg/m3,弹性模量为3.05×103 MPa。进行粮食立筒仓卸料仿真模拟时采取一次性卸料工况,P1~P5 为筒仓仓壁上创建的数据采集网格,用来采集贮料颗粒对仓壁产生的侧压力,测点深度从满仓装粮线开始算起,满仓装粮线为模型结构顶部向下0.1 m,P1、P2、P3、P4、P5 位置分别对应测点深度0.2、0.5、0.8、1.1、1.265 m 处;在与侧压力测点对应高度处设置颗粒网格组,V1~V5 用来采集与侧压力测点对应的不同高度处颗粒速度网格组数据,如图1 所示。
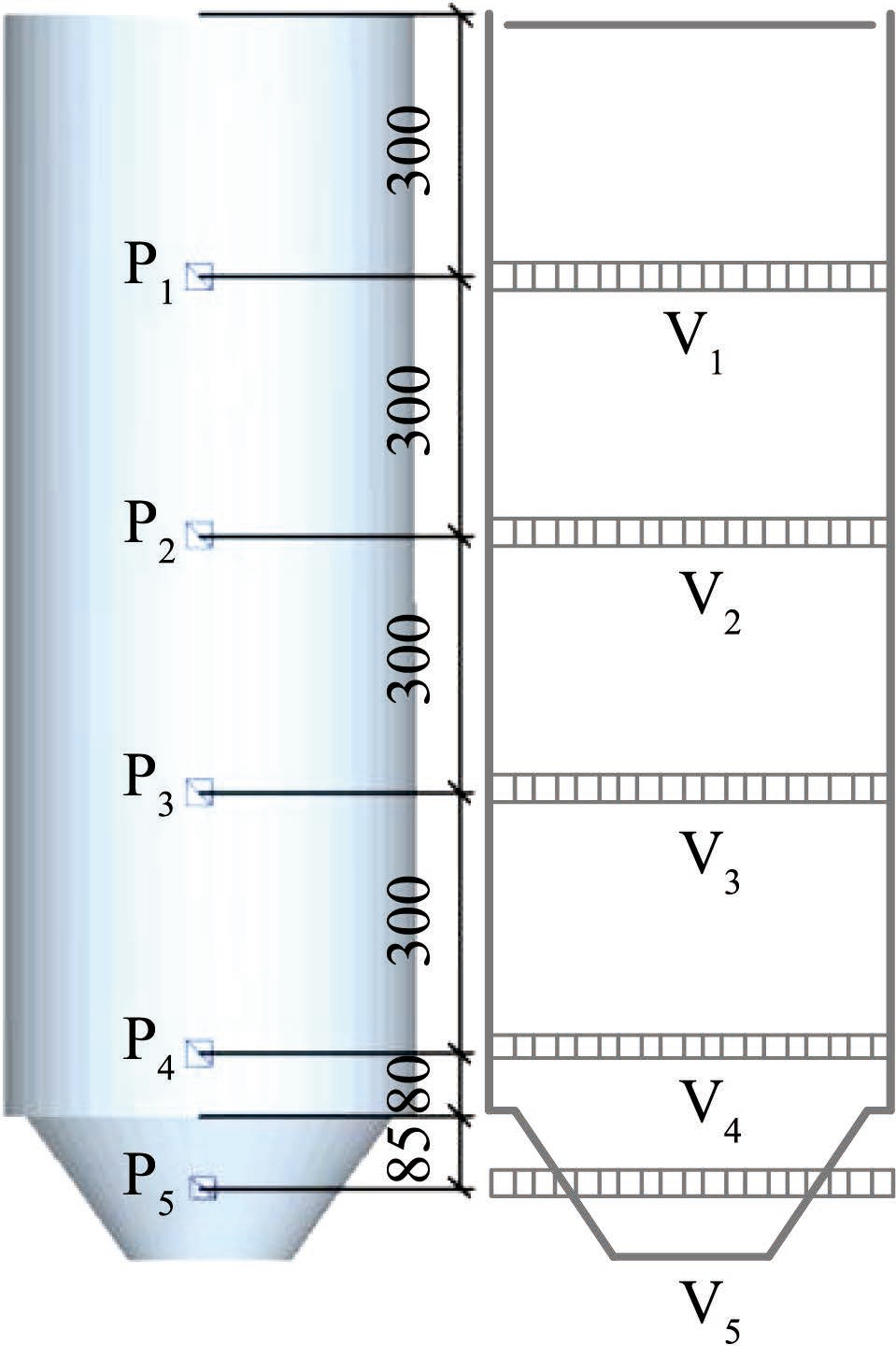
图1 立筒仓模型
Fig.1 Silo model
1.2 贮料选取
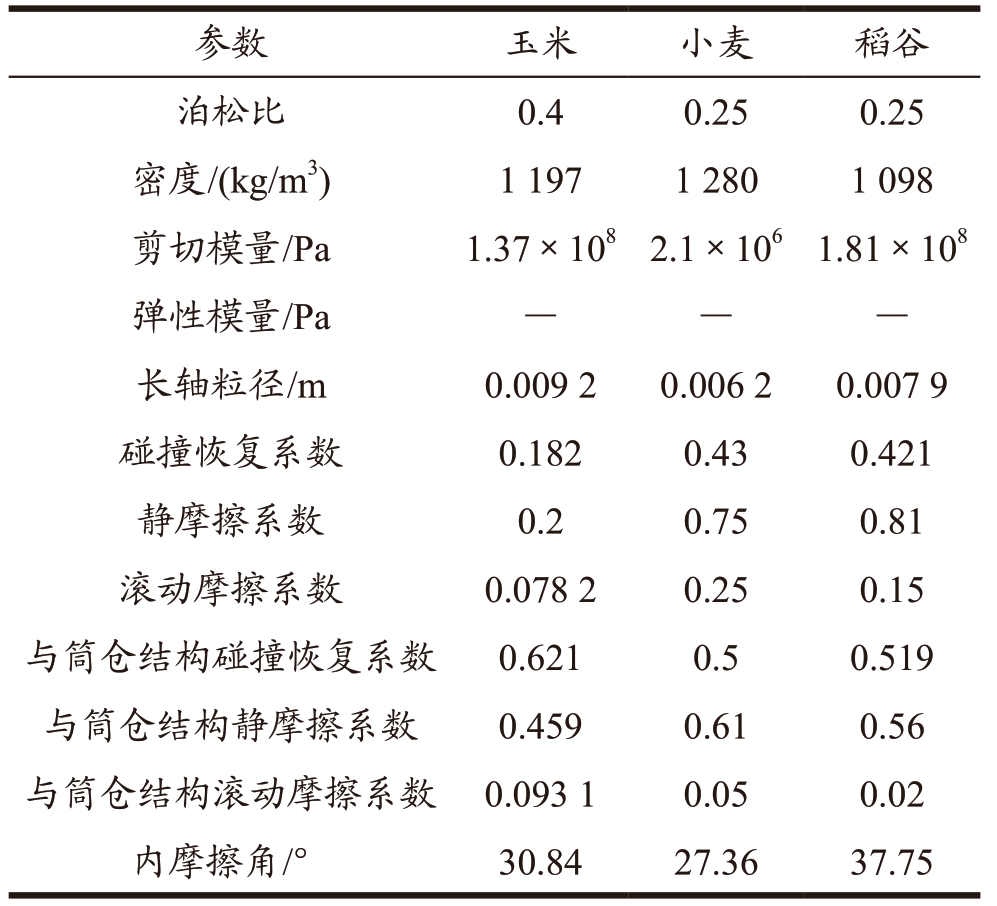
玉米、小麦和稻谷的物理特性与接触属性参数 [17-20] 如表1 所示。为了简化计算,本文模拟的不同贮料均采用圆形颗粒进行建模仿真,同时与试验 [16] 采用的陶珠颗粒进行对比分析。
表1 不同种类贮料仿真参数
Table 1 Simulation parameters for different types of storage
1.3 灰色关联度分析法
由于贮料散体的特殊性,不同种类的贮料,其物理特性与接触属性参数十分复杂,单纯考虑规范中的贮料参数存在一定的局限性,故结合EDEM 仿真模拟参数和结果,基于灰色关联度分析法 [21](Grey Relational Analysis,GRA)对影响筒仓动态侧压力因素进行分析。灰色关联度分析法通过计算灰色关联度,不需要大量数据样本,即可评估量化复杂系统中各种因素对系统性能的影响贡献度,识别出主要影响因素,该方法适用于分析立筒仓卸料时动态侧压力影响因素。
1)设参考数列为:
式中:
n——工况序号。
设比较数列为:
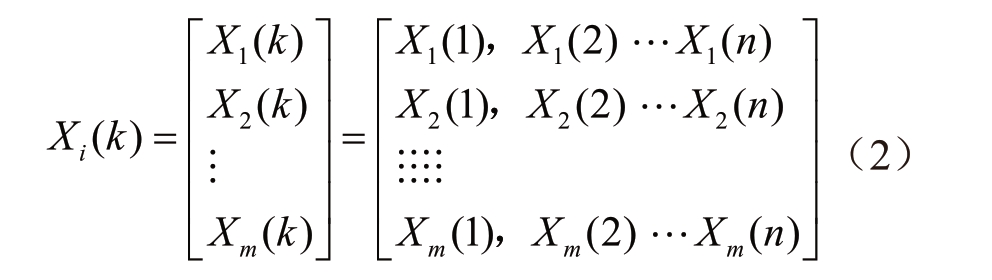
式中:
n——工况序号;
m——影响因素数量。
2)为了减少分析误差,利用下式对原始序列进行无量钢化:
3)计算关联系数:
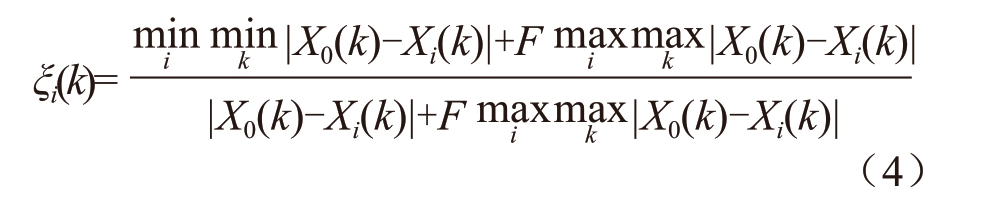
式中:
Δi(k)=|X0(k)-Xi(k)|为参考数列和比较数列的绝对差;
最小极差为![]() ,表示各比较数列与参考数列各点对应绝对差值中的最小值;
,表示各比较数列与参考数列各点对应绝对差值中的最小值;
最大极差为![]() ,意义同最小极差;
,意义同最小极差;
F——分辨系数,取值范围为0~1,其取值不能过大也过小,否则不能正确反映参数之间关联度,通常取0.5。
4)按照式(5)计算关联度,将各个时刻的关联系数求得平均值,其范围为 [0,1],越接近1 则表明该种因素对系统性能的影响程度越大,该种因素代表的比较数列与参考数列关联度越高。
5)将同一个参考数列对应的m 个比较数列的关联度按大小进行排序,即形成关联序。
超压系数是某一工况同一测点处的动态侧压力与静态侧压力的比值,故进行关联度分析时,将静态侧压力和动态侧压力值定为参考数列(母序列)代入式(1)。根据式(2),由10 个不同参数(见表1)定义比较数列(子序列),确定分析数列。通过式(3)将参考数列和比较数列原始数据进行无量纲化处理。计算参考数列与比较数列的绝对差、最小差值和最大差值,根据式(4)、(5)计算参考数列与比较数列的关联系数与关联度,作为各影响因素的比较数列对参考数列的关联度,并进行关联度排序,最终得出对静态侧压力和动态侧压力的影响关联度最大的影响因素。
2 结果与分析
2.1 仓体侧压力分析
2.1.1 不同种类贮料静态侧压力
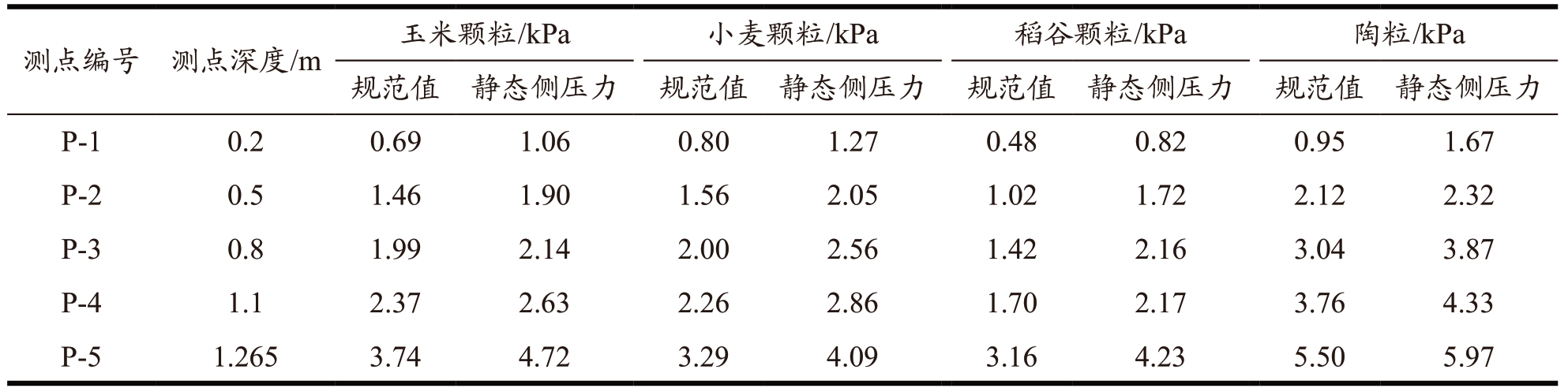
按照规范 [22] 中的式(6)计算不同种类贮料的静态侧压力,并提取EDEM 仿真模拟结果中装满贮料并静置后的静态侧压力,如表2 所示。
表2 不同种类贮料静态侧压力
Table 2 Static lateral pressure for different storage types
式中:
Ch——贮料水平压力修正系数;
γ——贮料的重度(kN/m3),取13.46 kN/m3;
ρ——筒仓水平净截面的水力半径(m),经计算取0.125 m;
e——自然对数的底;
s——贮料顶面至计算截面的距离,m;
μ——贮料对仓壁的摩擦系数,取0.264;
k=tan2(45°-φ/2)——侧压力系数,经计算取0.383 7;
φ——贮料的内摩擦角(°),取26.45°。
静态侧压力下陶粒的模拟值与试验 [16] 值接近,验证了柱承式立筒仓有限元模型的正确性与可行性,为玉米、小麦、稻谷三种贮料动态侧压力与超压系数及基于灰色关联度分析法的影响因素分析提供可靠的依据。
由表2 可知,玉米、小麦和稻谷的静态侧压力模拟值和规范值均随着测点深度的增加而增大,最大值出现在仓壁底部与漏斗连接范围内,同陶粒的静态侧压力试验值呈现一致的变化趋势;静态侧压力的模拟值均较大于规范值,其原因为在EDEM 生成贮料颗粒时,对颗粒施加了一定的初始速度,贮料装填更加密实导致静态侧压力大于规范值,同时规范公式计算值偏于保守。
2.1.2 不同种类贮料动态侧压力与超压系数
不同测点深度处的静态、动态侧压力,超压系数与规范中的水平侧压力修正系数Ch,如图2、图3 和表3 所示。
表3 不同种类贮料卸料时立筒仓侧压力及动态超压系数
Table 3 Silo lateral pressure and dynamic overpressure coefficient under different kinds of storage
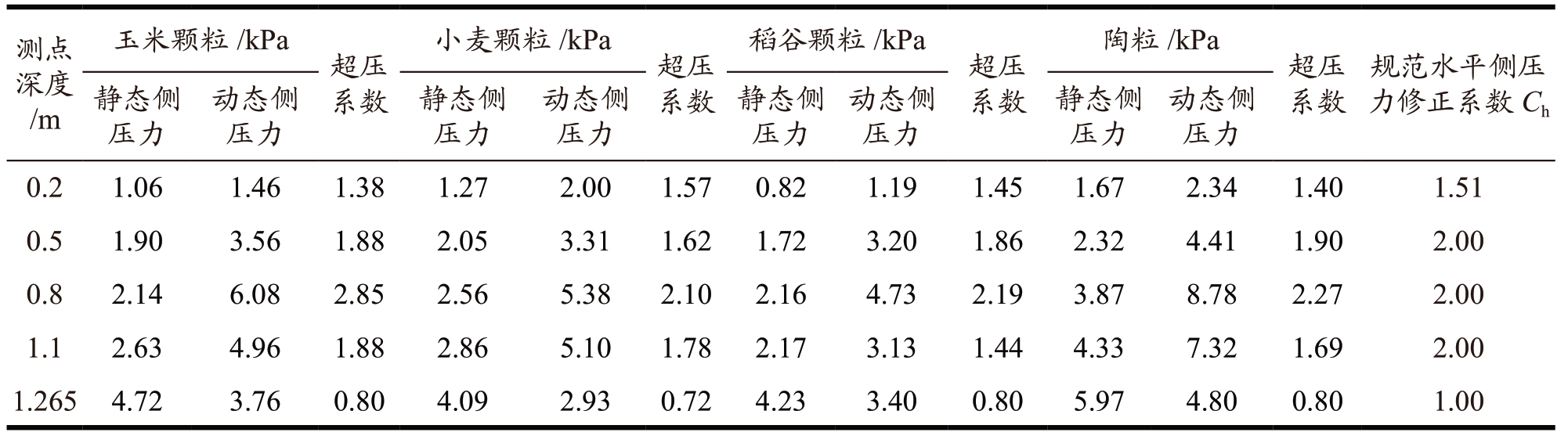
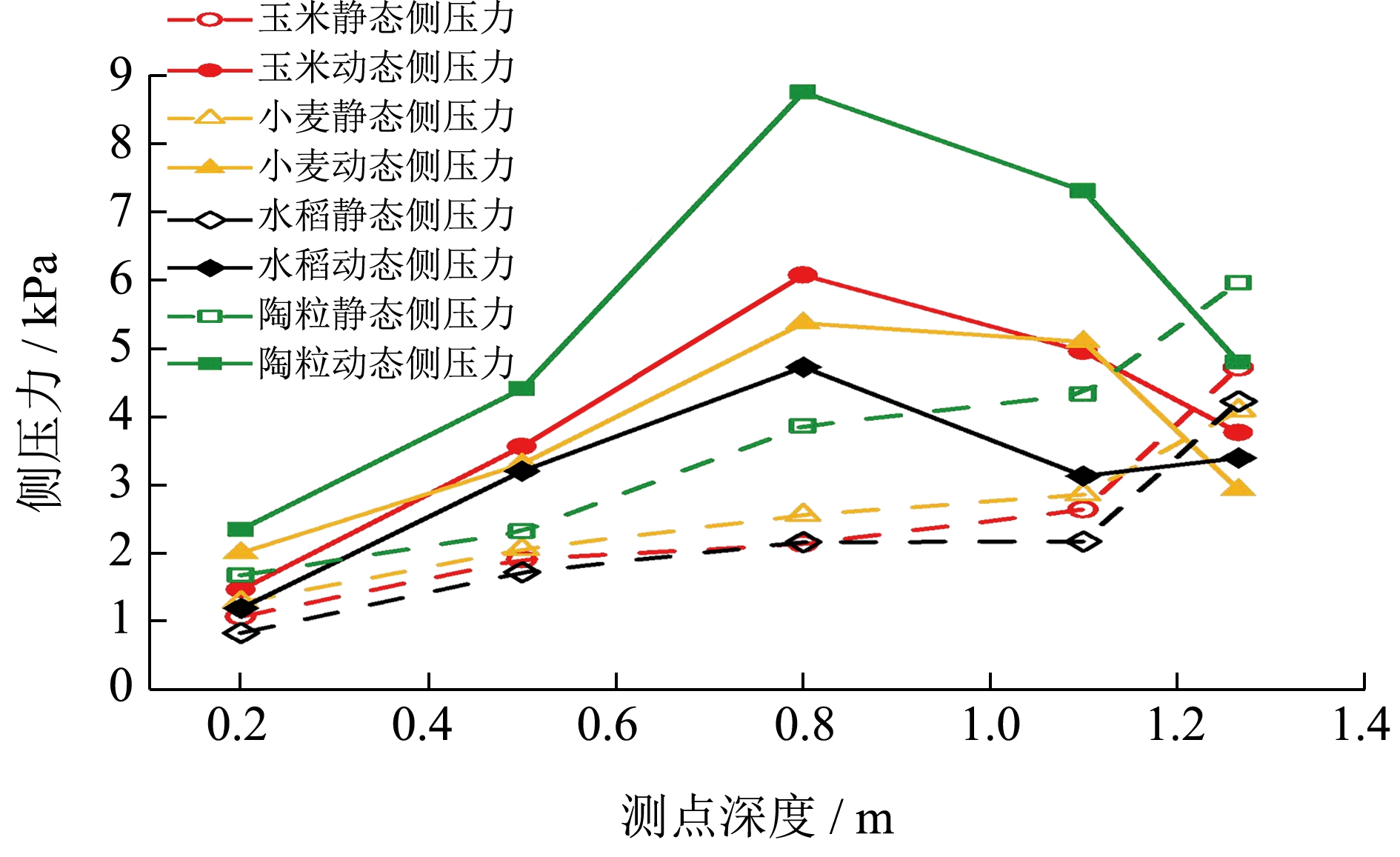
图2 立筒仓静态侧压力和动态侧压力图
Fig.2 Static lateral pressure and dynamic side pressure of vertical silos
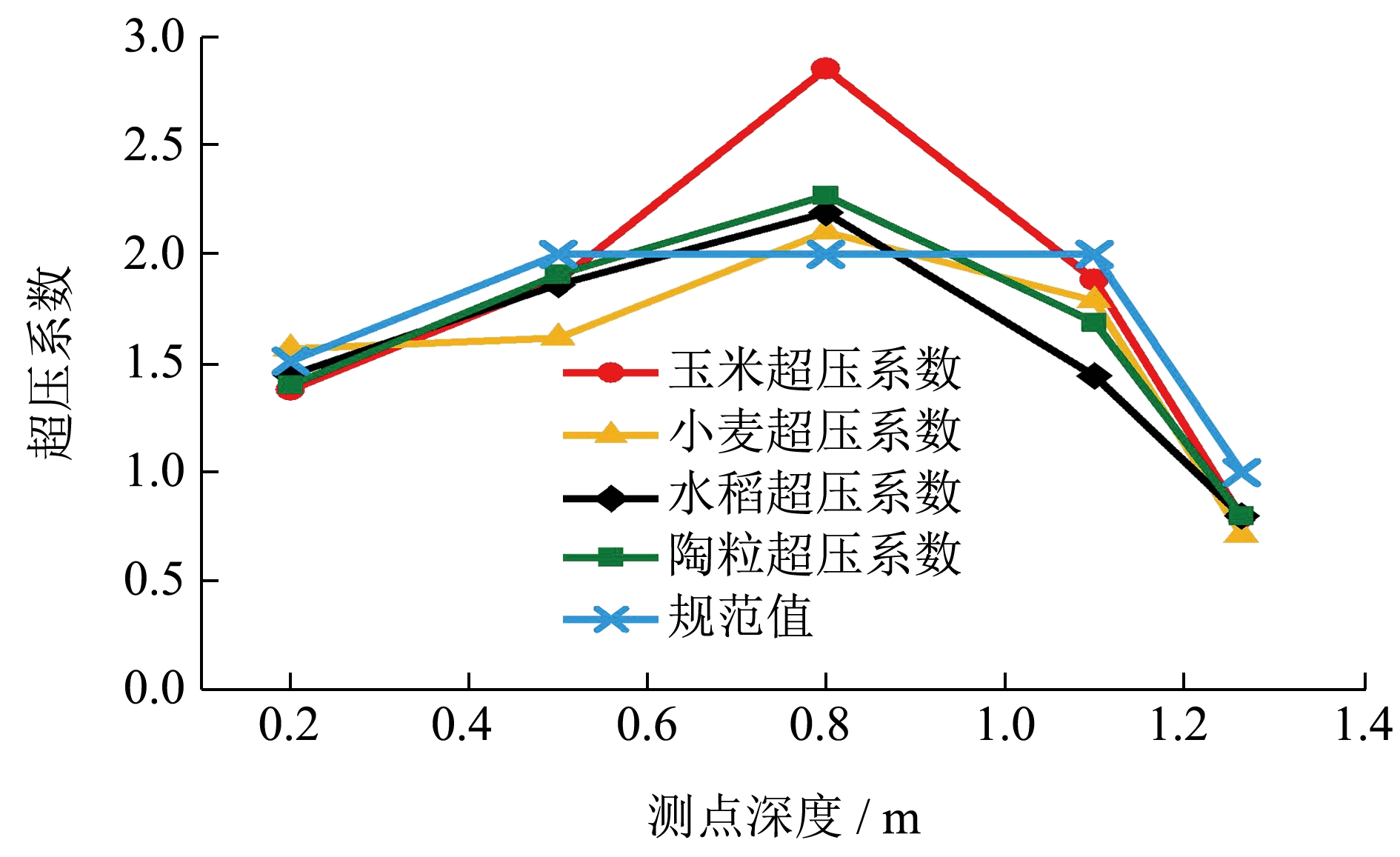
图3 立筒仓超压系数
Fig.3 Overpressure coefficient of vertical silos
通过图2、图3 以及表3 可知,对于不同种类贮料,筒仓仓壁各测点动态侧压力值相较于静态侧压力值均有不同程度的增加,存在超压现象,超压现象主要集中于筒仓仓壁下部1/3 范围内,且最大值发生在0.8 m 测点深度处;由于贮料的流动,贮料内出现成拱区域,上部贮料竖直向下对拱线施加荷载,使得颗粒之间、颗粒与仓体结构之间发生挤压和摩擦,从而引起仓壁侧压力增加,出现超压现象。玉米、小麦、稻谷和陶粒颗粒的动态侧压力分别达到6.08、5.38、4.73 和8.78 kPa,相应超压系数分别为2.85、2.10、2.19 和2.27,均超过规范中所规定的水平侧压力修正系数Ch=2.0,现行规范的水平侧压力修正系数是偏于不安全的。
2.2 流动状态与速度分布
由于卸料的流动状态与速度分布是密切相关的,对各不同种类贮料卸料过程中的竖向平均速度进行比较。通过建立的V1~V5 颗粒网格组,对整体卸料的贮料颗粒速度分布情况进行统计分析,所提取速度代表为某一时刻颗粒经过该网格组时的竖向平均速度。通过整体流量指数(MFI)对卸料流态进行量化分析。整体流量指数(MFI)为筒仓内壁边界处的贮料颗粒运动速度与筒仓内中心处的贮料颗粒运动速度之比。
图4 为不同高度处不同种类贮料竖向平均速度分布。在整体卸料过程中,不同贮料的中心速度均大于两侧仓壁的速度,并随着卸料的进行,图中的速度分布逐渐形成“漏斗状”。其中小麦贮料在V1-V4 位置处的速度均为最小,在V5 即漏斗处时,速度达到最大,超过了其它贮料的不同位置处的速度值,但是整体速度的数值差别不大。
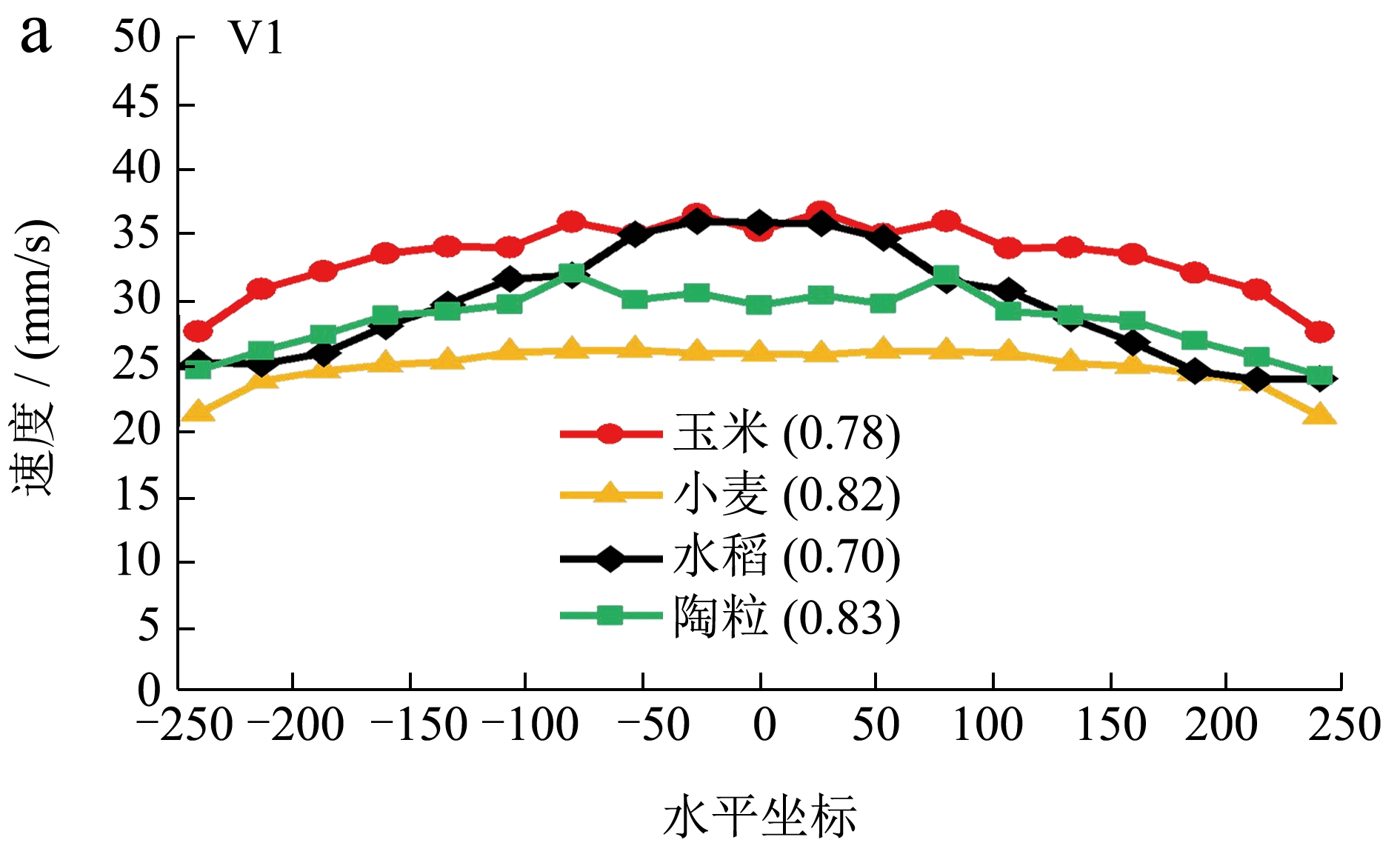
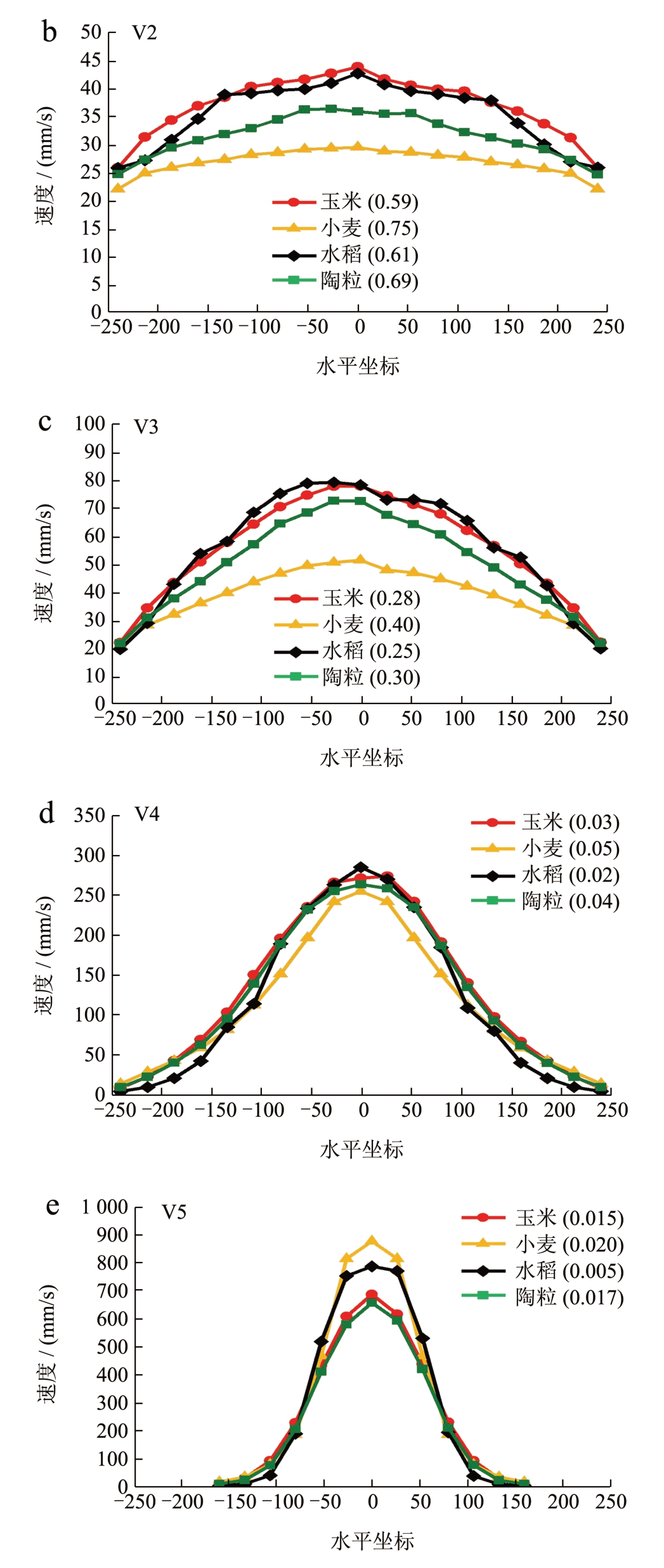
图4 不同高度处不同种类贮料竖向平均速度分布
Fig.4 Vertical average velocity distribution of different types of storage materials at different heights
注:MFI 值在括号中。
图5 为不同种类贮料MFI 值分布。卸料初始阶段,贮料流动状态为整体流,在V3 位置出现管状流动现象,并逐步转变为漏斗流状态,V4、V5 处则呈现出漏斗流状态;随着卸料的进行,逐渐呈现为管状流动,最后形成漏斗流,符合MFI 大于0.3时为整体流,小于0.3 时为漏斗流的判定。
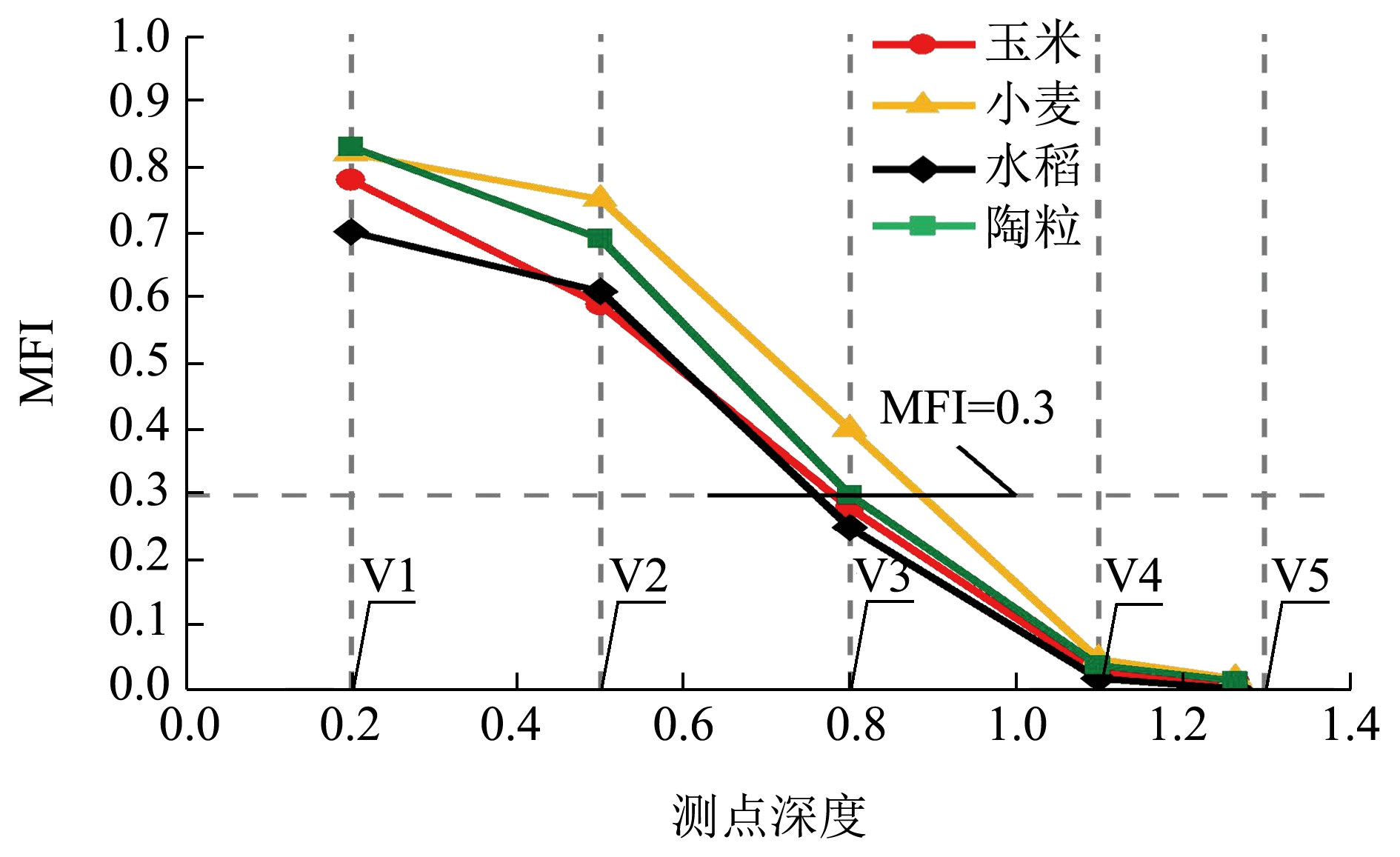
图5 不同种类贮料MFI 值分布
Fig.5 MFI value distribution for different types of storage
2.3 基于灰色关联度分析法的影响因素分析
根据本文上述研究分析,对于筒仓卸料时,超压现象主要集中于仓壁下部1/3 范围内,相对应测点深度0.8 m 处的超压系数最大,故进行关联度分析时,将0.8 m 测点深度处的静态侧压力和动态侧压力值定为参考数列(母序列)。
按照上述1.3 节计算方法及步骤,计算参考数列与比较数列的关联系数与关联度,计算结果如表4 所示,并进行关联度排序,如表5 所示。当参考数列为动态侧压力时,计算出以上相同的各影响因素对参考数列的关联度并进行排序,如表6 所示。
表4 参考数列与比较数列的关联系数与关联度
Table 4 The correlation coefficients and correlation degrees between the reference series and the comparison series
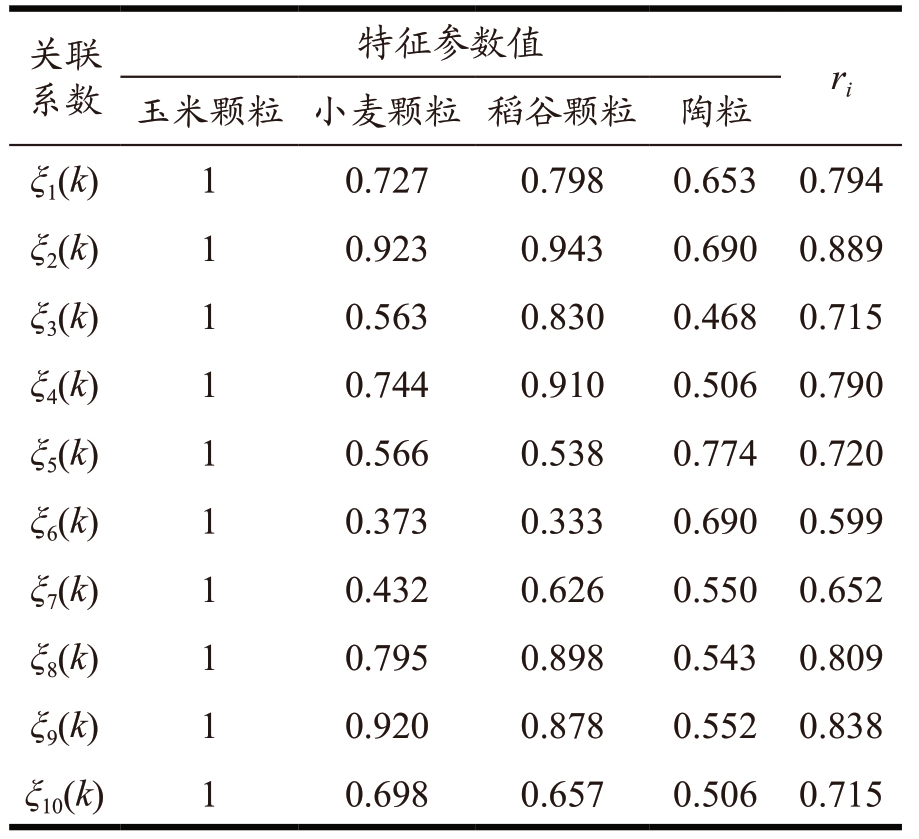
表5 各影响因素与静态侧压力的关联度
Table 5 Correlation degree between each influencing factor and static lateral pressure
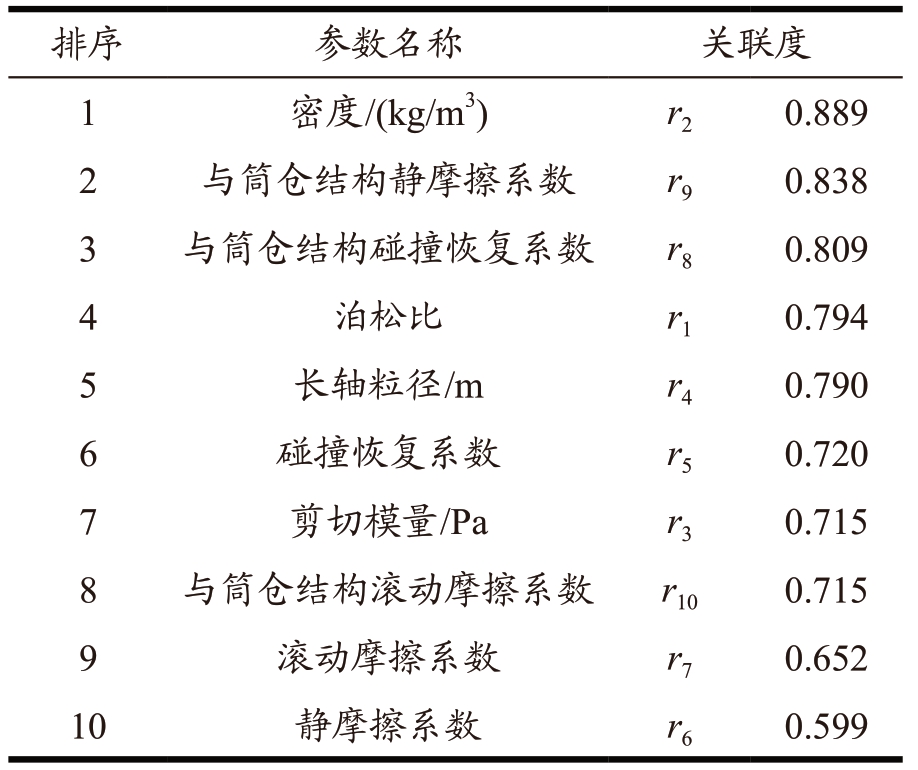
表6 各影响因素与动态侧压力的关联度
Table 6 Correlation degree between each influencing factor and dynamic lateral pressure
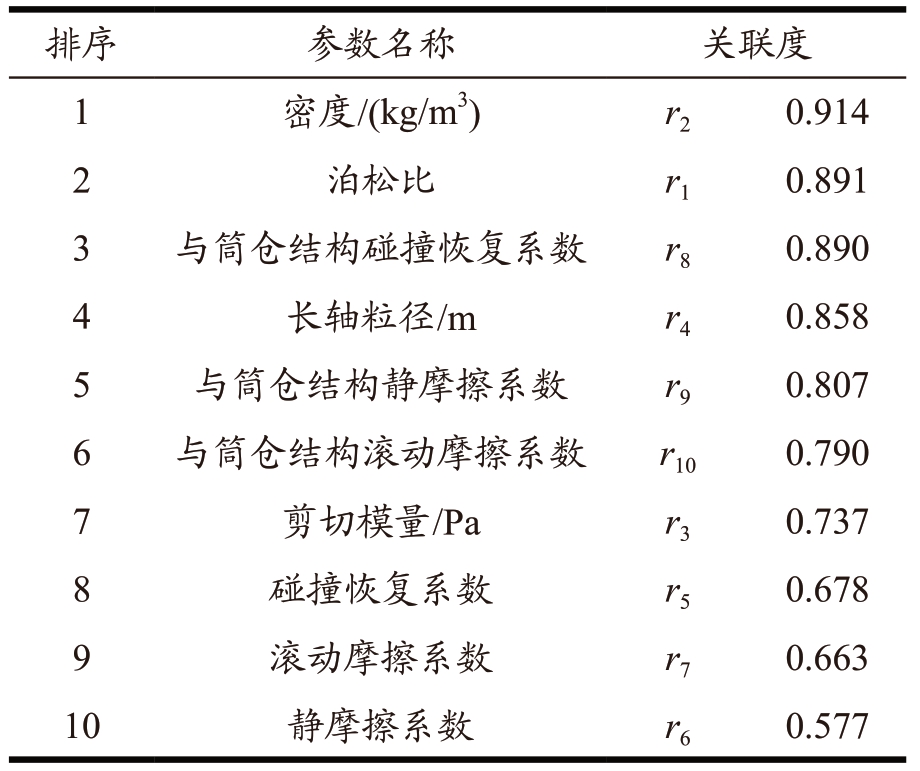
由表5、表6 可知,静态侧压力和动态侧压力的影响因素关联度在0.8 以上的有密度、贮料与筒仓结构静摩擦系数和贮料与筒仓结构碰撞恢复系数;贮料密度对静态侧压力、动态侧压力的影响关联度最强、贡献度最大。碰撞恢复系数是反映贮料颗粒与物体发生接触碰撞变形后能够自我恢复到原始状态的能力,该因素同时影响着筒仓装料时的静态侧压力和筒仓卸料时的动态侧压力。
设计筒仓结构时,规范 [22] 中静态侧压力计算公式已考虑贮料密度和贮料与结构摩擦系数的影响,但尚未考虑贮料与筒仓结构的碰撞恢复系数,故在设计筒仓时,可考虑贮料与结构碰撞恢复特性的影响。
3 结论
本文采用EDEM 仿真模拟软件,选取不同种类贮料进行粮食立筒仓卸料模拟,分析其静态侧压力、动态侧压力分布规律和相应超压系数、流动状态与速度分布关系,并基于灰色关联度方法进行影响因素分析,主要结论如下:三种贮料的静态侧压力模拟值大于规范值,规范公式计算值偏于保守;不同种类贮料的动态侧压力超压现象集中于筒仓仓壁下部1/3 范围内,且最大值发生在0.8 m 测点深度处且均超过规范中所要求的水平侧压力修正系数,现行规范中水平侧压力修正系数偏于不安全;基于灰色关联度分析法得出,贮料密度、贮料与筒仓结构静摩擦系数和贮料与筒仓结构碰撞恢复系数是影响静态、动态侧压力的主要因素。目前筒仓规范中缺少对贮料与筒仓结构的碰撞恢复系数的提及与分析,在设计筒仓时,可考虑贮料与结构碰撞恢复特性的影响。
[1] KOBYLKA R,MOLENDA M.DEM simulations of loads on obstruction attached to the wall of a model grain silo and of flow disturbance around the obstruction [J] .Powder Technology,2014,256:210-216.
[2] GALLEGO E,RUIZ A,AGUADO P J.Simulation of silo filling and discharge using ANSYS and comparison with experimental data [J] .Computers and Electronics in Agriculture,2015,118:281-289.
[3] LI Y,GUI N,YANG X T,et al.Effect of friction on pebble flow pattern in pebble bed reactor [J] .Annals of Nuclear Energy,2016,94:32-43.
[4] 钟佳,吕慧,曹贵平,等.细颗粒在锥形和平底料仓中的重力卸料特性 [J] .化工进展,2017,36(11):3940-3946.
[5] 孙栋,陆海峰,曹嘉琨,等.复杂流道结构料仓的下料流率预测 [J] .化工学报,2020,71(3):974-982.
[6] 翟志轩,熊丽敏,苏文献.料仓卸料流动特性及结构强度数值模拟研究 [J] .化工设备与管道,2021,58(2):35-42.
[7] 徐志军,程远浩,原方,等.流槽对筒仓双侧壁卸料动态压力分布影响研究 [J] .中国粮油学报,2021,36(5):135-141.
[8] 赵光明,程远浩.基于PFC模拟的曲线漏斗筒仓动态压力研究 [J] .特种结构,2022,39(5):74-77.
[9] SUN W W,ZHU J P,ZHANG X D,et al.Multi-scale experimental study on filling and discharge of squat silos with aboveground conveying channels [J] .Journal of Stored Products Research,2020,88:101679.
[10] GANDIA R M,OLIVEIRA J E A,GOMES F C,et al.Experimental pressures exerted by maize in slender cylindrical silo:comparison with ISO 11697 [J] .Engenharia Agrícola,2021,41:576-590.
[11] GANDIA R M,GOMES F C,de PAULA W C,et al.Static and dynamic pressure measurements of maize grain in silos under different conditions [J] .Biosystems Engineering,2021,209:180-199.
[12] 郭健玮,孔建益,王兴东,等.中心口锥底料罐中离散颗粒卸料特性的实验与仿真研究 [J] .武汉科技大学学报,2018,41(3):206-211.
[13] 冯永,原子然.基于改进颗粒簇单元的卸粮宏细观机理模拟 [J] .中国粮油学报,2019,34(10):69-76.
[14] 周剑萍,杜泽鹏.湿颗粒材料筒仓卸料过程的离散元模拟 [J] .重庆大学学报,2020,43(6):58-64.
[15] 吴承霞,徐志军,庞照昆,等.基于不同贮料的筒仓侧压力试验与数值模拟 [J] .工业建筑,2021,51(8):68-73.
[16] 丁永刚,孙启帅,刘强,等.分层卸料时粮食立筒仓动态侧压力试验研究 [J] .河南工业大学学报(自然科学版),2022,43(1):113-120.
[17] 谭援强,肖湘武,郑军辉,等.锥形改流体下部孔径对筒仓卸料流态的影响 [J] .农业工程学报,2016,32(19):82-87.
[18] 刘瑞,李衍军,刘忠军,等.包衣玉米种子离散元参数分析与标定 [J] .农业机械学报,2021,52(S1):1-8,18.
[19] 姚小旭.粮食物理参数的实验研究 [D] .郑州:河南工业大学,2019.
[20] 邱白晶,姜国微,杨宁,等.水稻籽粒流对承载板冲击过程离散元分析 [J] .农业工程学报,2012,28(3):44-49.
[21] 刘思峰.灰色系统理论及其应用 [M] .第9版.北京:科学出版社,2021.
[22] GB50077-2017,钢筋混凝土筒仓设计标准 [S] .